Forecasting the Candidates
(16 Mar 2020) Data and code are available on Github.
On Monday, the 2020 Candidates tournament kicks off in Yekaterinburg. Seven badly dressed young men and Alexander Grischuk are going to play 56 games of chess over two weeks. Most will end in a draw, so four cascading tournament tie-break rules are on stand-by. The eventual winner gets to live the next several months in a daze of LED light, caffeine and false hope before being the guest of honour at Magnus Carlsen’s re-coronation in Autumn. In preparation for this exdrawaganza, I built a simple model of chess player strength and used it to forecast the outcome of the tournament. The well-established Elo system can also be used for this purpose and may even yield better predictions. My aim was not to compete with Elo, but to try my hand at modelling of chess and get a sense of what could be possible both in terms of data and statistics.
From the excellent live Elo site 2700chess.com I compiled a record of 2700+ on 2700+ violence since 30 November 2016, the day Sergey Karjakin lost his championship match to Carlsen. A nice feature of the dataset is that for every game the opening played is also recorded in the form of the ECO code. I tried to filter out rapid and blitz games, but many remain, in particular from the most recent World Cup. Overall, I ended up with 3266 games between just 66 players. Perhaps all this time they spend together explains the uniformly unconscionable wardrobes.
Davidson ratings
My model is based on Davidson ratings, an extension of the much better known Bradley-Terry model. The rating of each player is a number between 0 and 1 such that for any two players, the ratio of their ratings is the ratio of their respective probabilities of winning the encounter. A single additional parameter controls the rate of draws. I first saw Davidson ratings applied in the sport context on the excellent opisthekota blog, where it was used to analyse the more plebeian disciplines of “handball” and “football”. The only modification to the original model that I made was to make the draw parameter depend on the ECO code. In this way, I hoped to capture “drawishness” of openings. As is my usual MO, I implemented and fitted the model in Stan.
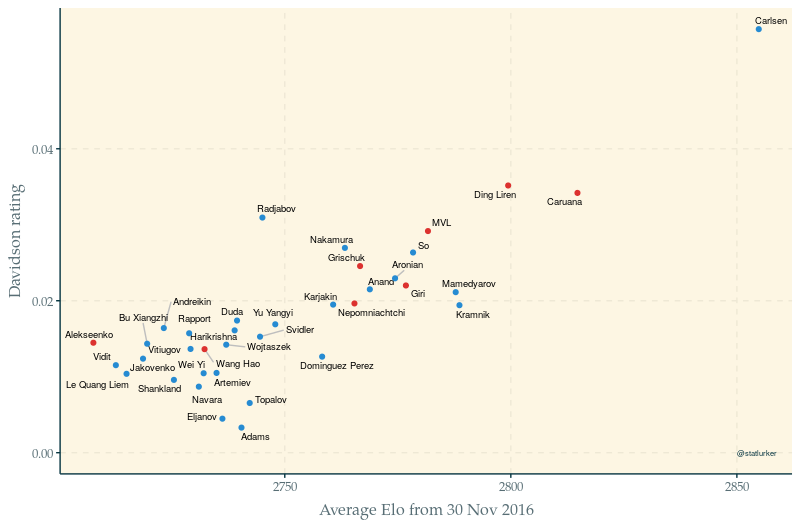
The figure above shows the ratings scattered against the average Elo for the same period. As expected, there is a correlation – so far so good. Magnus Carlsen is head and shoulders above everyone else, of course, with Caruana and Ding Liren peeling away from the rest of the pack. Interestingly, my model rates Caruana and Ding as almost exactly equal in strength. Thanks to his World Cup win, Teimour Radjabov is also very highly rated. But the best way to compare both rating systems is in the context of a match-up, so let’s instead look at what both systems think would happen if everyone ganged up on the biggest nerd:
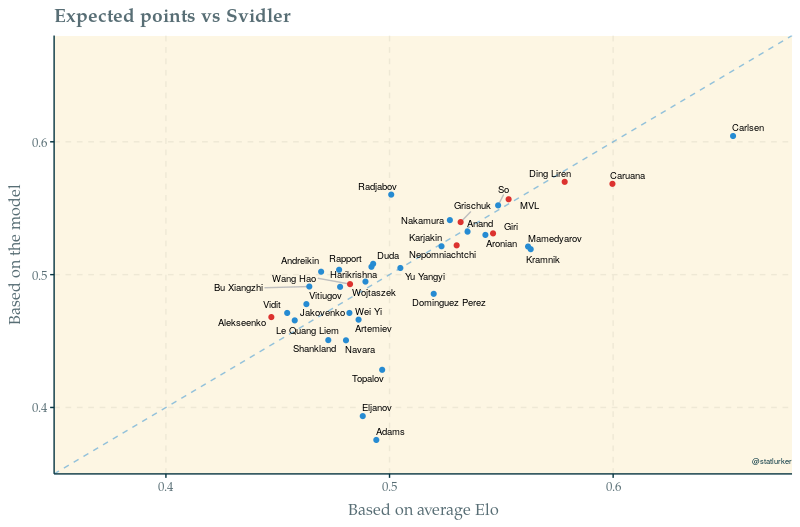
Both rating systems broadly agree on players’ chances in a hypothetical match-up against Peter Svidler. The Davidson model does not rate Topalov, Eljanov and Adams and (again) overrates Radjabov. Most of the players stronger than Svidler fall below the dashed equality line, indicating that the Elo system gives them better odds than my model. It turns out that it is not an accident: the Davidson likes favourites less than Elo does. This is nowhere more evident than when facing Carlsen:
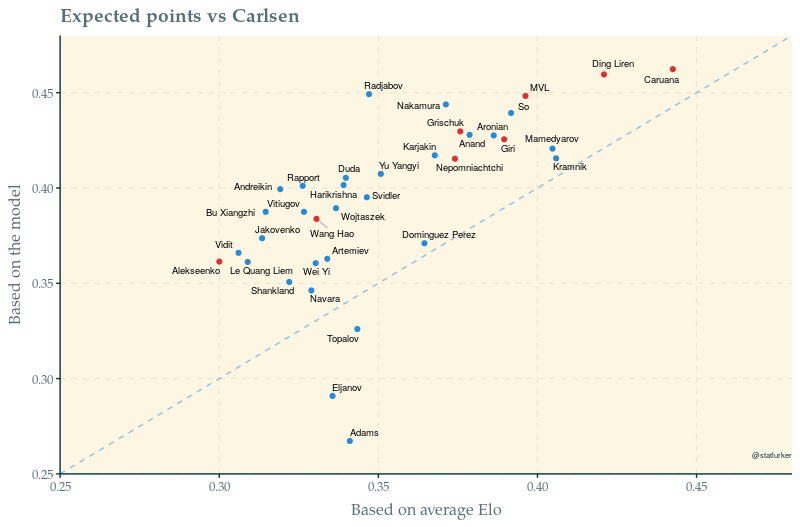
Everyone except the three weakest players is now predicted to do better against Carlsen than Elo would have us believe. This striking result should be taken with a pinch of salt – the comparison is based on average Elo and the dataset still has blitz and rapid games in it. But it may be a sign that Elo is not well suited to rating elite players. If so, then Carlsen has been forced to drive up the 2900 hill with a handbrake on.
Draws and openings
As mentioned before, I modified the original Davidson model to take the opening information into account. I did it in the quickest and least creative way possible, simply making the parameter controlling the draw propensity depend on the ECO code. The reality of opening theory and elite game preparation is of course infinitely more complex. From the modelling perspective, when the strongest or weakest players prefer certain openings, these will appear to the model as less drawish than they objectively are. Still, the results are interesting:
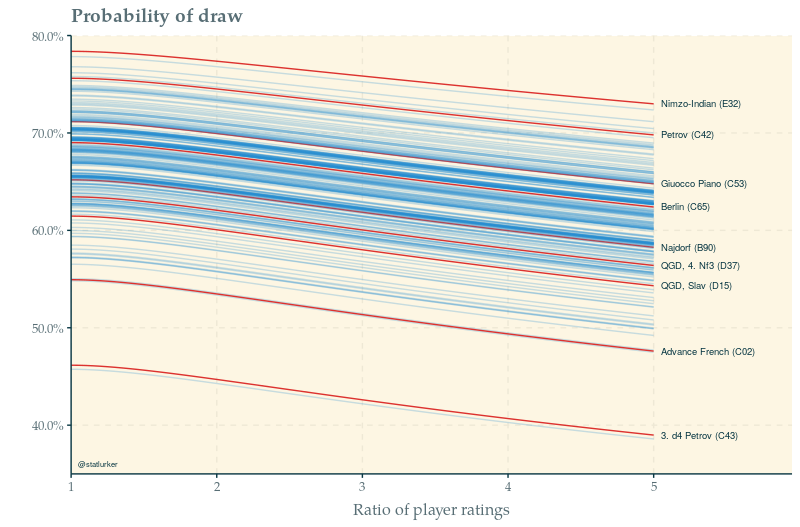
In a game between two evenly matched players (i.e. with the ratio of ratings exactly equal to 1), the model predicts a draw 68% of the time. When one player is 5 times more likely to win than the other (rating ratio of 5, roughly Carlsen vs Vidit), the probability of a draw is a mere 61%. But that’s just on average – as the plot shows, there is considerable variation across openings. The Nimzo-Indian is confirmed as the safest of Black’s choices. The two subspecies of Petrov are diametrically opposed: the C42 cluster is rated as one of the most drawish openings, while the C43 modern attack with 3. d4 as one of the least – the result of the sucesses that the Candidates Caruana and Wang Hao have had with it, and of Yu Yangyi’s insistence on getting beaten in this line.
Simulating the 2020 Candidates
With all these preliminaries out of the way, let’s predict the Candidates! I took the fitted model and simulated the tournament 10’000 times. Here are the results:
| Player | Winning sims | Win probability | Win odds |
|---|---|---|---|
| Ding Liren | 2367 | 23.8% | 4.20 |
| Caruana | 2216 | 22.3% | 4.48 |
| MVL | 1734 | 17.5% | 5.71 |
| Grischuk | 1220 | 12.3% | 8.13 |
| Giri | 991 | 10.0% | 10.0 |
| Nepomniachtchi | 829 | 8.3% | 12.0 |
| Wang Hao | 381 | 3.8% | 26.3 |
| Alekseenko | 196 | 2.0% | 50.0 |
A quick check reveals that the betting market disagrees quite strongly, preferring the favourites much more. This makes sense: the markets are almost certainly aligned with Elo-based predictions, and these are tilted towards favourites compared to my model. The Elo-based odds will also correctly use the most recent Elo ratings, while the model treats playing strength as constant over 2016-2020. The blitz and rapid games from my dataset further confuse the issue. In conclusion, your money will be better spent in your local cheese shop than at the bookies.
In the interest of full disclosure, I should say that in 66 (0.7%) of the simulations the tournament was still tied after the first three tie-breaks (head-to-head, number of wins and Sonneborn-Berger) were applied. Implementing multi-way head-to-head ranking made me question my life choices and Sonneborn-Berger threatened my sanity outright, so I stopped short of implementing playoffs and instead just discarded these simulations. This probably hurts the underdogs, whose path to victory leads though draws and tiebreaks to a larger extent than that of the favourites, but the bias is tiny compared to the larger data and design issues mentioned before.
Since at the time of writing it is quite possible that the tournament and/or humanity will be cancelled, I humbly offer a random single simulation as the substitute outcome. It turns out that Ding put in a career-defining performance and can look forward to being ritually mauled by Carlsen later in the year:
| player | points | wins | HTH | SB |
|---|---|---|---|---|
| Ding Liren | 10 | 7 | 65.0 | |
| MVL | 8 | 3 | 54.0 | |
| Caruana | 7.5 | 3 | 49.2 | |
| Grischuk | 7 | 2 | 1 | 47.2 |
| Nepomniachtchi | 7 | 1 | 1 | 46.8 |
| Giri | 6.5 | 2 | 40.8 | |
| Wang Hao | 5.5 | 2 | 35.8 | |
| Alekseenko | 4.5 | 0 | 34.2 |
Bonus: the chess24 fantasy chess contest
chess24.com is a leading chess platform producing excellent chess content and arguably the best live commentary in the business. For the 2020 Candidates, they set fire to the last part by employing Nigel Short and Lawrence Trent, and expanded into fantasy sports instead. While I refuse to put a single actual Swiss frank on the predictions of my model, I value my time so little that I wrangled my simulation data to help me make some of the selections. I record them here, together with the expected points:
| Item | Selection | xP | Note |
|---|---|---|---|
| Who will win the 2020 Candidates Tournament? | MVL | 10.5 | |
| Pick a player. Every time they win a game you get the number of points in the parenthesis | Giri | 11.7 | FML |
| Pick a player. Every time they win a game, you get the number of points in the parenthesis (part deux) | MVL | 10.9 | |
| Pick a player. Every time they lose a game, you get the number of points in the parenthesis | Caruana | 14.2 | |
| Pick a player. Every time they draw a game, you get the number of points in the parenthesis | Nepo | 10.9 | very close |
| Will there be a tie for first place after 14 rounds? | No | 1.50 | |
| Who will finish with a better score? | Grischuk | 2.05 | |
| Will both games between Caruana and Ding end in draws? | No | 3.81 | not close |
| What will Giri’s final score be? | +1 or better | 1.25 | close |
| What will Vachier-Lagrave’s final score be? | +1 or better | 1.64 | not close |
| Will Alekseenko finish in last place or in a tie for last place? | No | 1.33 | |
| Tiebreaker Question: Out of 56 games, how many decisive games will there be in the entire tournament? | 19 |
With thanks to Thom Lawrence and James Yorke for inspiration and feedback.